Introduction

The development of systems for describing human movements is a relevant task across various fields, such as choreography, robotics, animation, and many others. Just as a musical score represents musical notes, movement notation is designed to provide precise instructions regarding specific movements, actions, as well as their combinations and/or sequences. The creation of notations that describe movements across different domains faces several challenges. The first challenge is the absence of a universal language for recording movements. Different fields use distinct methods and languages to record movements, leading to a “Tower of Babel” situation where communication between disciplines becomes difficult (Laumond, Abe, 2016). The second challenge arises from the established terminological systems, paradigms, and goals in different fields (e.g., choreography vs. robotics), which further complicates interdisciplinary communication and hinders scientific integration (Calvert, 2015).

At the same time, the metalinguistic and conceptual fragmentation of disciplinary fields contradicts the qualitative changes in the nature of human communication and activity, driven by the increasing prominence of interface-mediated communication and the digitization of various forms of activity. This type of communication demands universal “seamless” tools (meta-languages and technologies) for transitioning between different forms of human activity. Hence, there is a need to explore new, potentially universal approaches to describing human-machine interaction (HMI) and human-computer interaction (HCI).

Electronic computing devices and virtual anthropomorphic 3D models, such as robots and virtual avatars, imitate human behavior, communication, emotions, movements, gestures, and other human traits and behavioral patterns. As these anthropomorphic models become more integrated into everyday life, they must be able to handle a wide range of human actions and linguistic expressions. When discussing human movements, for effective interaction with people and the extraction of information from linguistic and gestural data, these intelligent models need to understand the referential relationships between actions and language, as well as interpret actions conveyed through language.

The development of tangible human-machine interfaces is based on the principles of human communication, where information is perceived, processed, and transmitted using multiple modalities (Belousov et al., 2024). Semantics in this context covers not only auditory or visual messages but also motor actions. For example, van Elk et al. describe the semantics of actions as a hierarchically organized system, whose subsystems are selectively activated depending on the subject’s intentions and task context (van Elk et al., 2009). In natural communication, information is transmitted through several channels of different modalities to “narrow” and focus the scope of meaning. For instance, spatial deixis in face-to-face interaction requires gestural involvement: “Look there!” (accompanied by a hand gesture or a nod).

Typically, the problem of describing movements relates to the discussion of the differences between movements and gestures. Several approaches distinguish between movement and gesture. For example, movement can be viewed as a concept encompassing any physical activity of the body, including gestures, which, in turn, carry symbolic meaning in communication (Bull, Doody, 2013; Kendon, 1997; Kilpatrick, 2020; Murillo et al., 2021; Novack, Wakefield, 2016: 340; Stults-Kolehmainen, 2023). According to the approach of A.M. Novack et al., a gesture is not directly related to altering the world (e.g., opening a jar by twisting it) or representing movement patterns (e.g., performing dance steps). Instead, it represents movement that may change the world (e.g., a gesture showing how to open a jar by twisting it) or represents movement that exists on its own (e.g., a gesture showing how to perform a dance) (Novack, Wakefield, 2016: 340). Both examples are generally correct; however, one can find contexts where dance movements or opening a jar can be viewed as gestures. For example, professional dance movements (e.g., in ballet) are loaded with communicative and semantic meaning, and when directed at an audience, they are interpreted similarly to any other sign. The example involving material transformation of the world (“opening a jar”, etc.) can also be contextualized as a sign of professional skill.

We prefer an understanding of the relationship between gesture and movement, where movement is not only a general concept for gesture but also unites them in sequential chains (Kendon, 1997; Kilpatrick, 2020; Streeck, 2010; Trujillo et al., 2018). If a movement fragment is communicatively directed and semantically coherent, it can be considered a gesture. However, the same movement might not be a gesture if it lacks an addressee capable of interpreting the sign (with the addressee potentially being the communicator themselves, i.e., in the case of self-communication).

In the modern technological world, gestures are forms of non-verbal communication used not only for interacting with people but also with anthropomorphic virtual or robotic models. Recording human movements, developing models and algorithms for effective motion recognition, creating unified movement notation, and improving human-machine communication are pressing challenges in science, robotics, machine learning, and other fields.

The goals of movement notation – whether in dance, animation, or robotics – include providing clear, interpretable instructions that can be executed by performers, machines, or digital characters. Accurate movement notation is essential for their present and future use, study, or reproduction, ensuring consistency across different situations and among different performers (both human and anthropomorphic models). In this paper, we present a new concept and software solution for modeling and generating movements based on a semantically-oriented linguistic notation, which we have named the Perm Gesture Notation (PGN). The primary goal of this paper is to present a methodology for modeling human movements based on the developed linguistic notation. This includes the presentation of the developed notation, a description of an application that implements a movement control system based on the Blender 4.2 engine. In the developed application, visualization and generation of movements for anthropomorphic models, as well as compositional and sequential control of the generated movements based on the developed notation, are carried out. To achieve plausible anthropomorphic behavior in the 3D model, we use a multimodal corpus of audiovisual recordings of people describing various emotional states. This confirms the possibility of modeling a wide range of human motor actions.

Theoretical review

The development of movement notation systems has a history spanning several centuries. Since the 15th century, at least 87 different movement notation systems have been used across Europe and North America (Abbie, 1974; Farnell, 1996; Guest, 1984; Key, 1977). These systems often arose to document specific dance styles or gesture languages, and many fell out of use as the associated movement practices evolved or disappeared (Farnell, 1996).

In the field of non-verbal communication research, any attempt to develop a movement alphabet must inevitably take into account historically significant systems of movement notation, including the Beauchamp-Feuillet system that thrived at the French court in the 17th and 18th centuries, Gilbert Austin’s gesture system for public speaking from 1806, Ray Birdwhistell’s kinesics from the mid-20th century, William Stokoe’s system for recording American Sign Language, as well as adaptations for other sign languages by Adam Kendon and La Mont West Jr. Generalized systems like Labanotation, Laban Movement Analysis, Benesh Choreology, and Eshkol-Wachman notation are designed for adaptation to a wide range of movements, functioning as a “phonetic alphabet” for body actions, capable of recording any physical action while preserving its semantic content (Abbie, 1974; Bashan et al., 2024; Benesh, Benesh, 1956; Bernardet et al., 2019; Birdwhistell, 1952; Dell, 1977; El Raheb, Ioannidis, 2014; El Raheb et al., 2023; Eshkol, Wachmann, 1958; Farnell, 1996; Frishberg, 1983; Grushkin, 2017; Guest, 1984; 2005; Harrigan, 2008; Kendon, 1997; Key, 1977; Laban, Lawrence, 1974).

Several key systems of movement description have emerged from related fields such as anthropology, ethology, and psychology. The Facial Action Coding System (FACS) (Ekman, Friesen, 1978) is designed for analyzing and interpreting facial expressions by identifying specific facial actions. The Bernese System (Frey et al., 1982) offers a methodology for analyzing movement in psychological and anthropological studies. The most recent system, the Body Action and Posture Coding System (BAP) (Dael et al., 2012), was developed for detailed analysis of body movements and postures using 141 behavioral variables that capture complex temporal movement segments. These systems provide a comprehensive toolkit for studying non-verbal communication and human behavior in various scientific and applied contexts (Bernardet et al., 2019).

Movement classification, coding, and interpretation systems differ across several parameters, including their intended purpose, origin, level of detail, and reliability. First, these systems vary in their objectives: some are designed for reproducing or analyzing movements, while others aim to draw conclusions about the individual performing the movements. For example, systems originating in dance, such as Labanotation and Laban Movement Analysis, focus on the precise transmission and analysis of dancers’ movements. In contrast, systems from anthropology, ethology, and psychology, like FACS and kinesics, are aimed at studying and interpreting human behavior in a broader context (Birdwhistell, 1952; Bernardet et al., 2019; Duprey et al., 2017; Ekman, Friesen, 1978; Laban et al., 1974).

Second, the level of subjective inference varies among different systems. Some systems rely on subjective judgments by coders, while others use systematic labels and observational coding, or direct measurement of muscle activity. This distinction is particularly important in scientific research, where high precision and data reliability are required (Bernardet et al., 2019).

The focus on movement quality or type is another distinguishing feature of various systems. For instance, Labanotation and the Bernese System emphasize movement quality, while kinesics focuses on types of movements. The level of system detail, including parameters such as the minimum time unit for coding, the size of the alphabet (number of distinct codes), and the number of simultaneously coded tracks (body parts), plays a key role in determining the system’s level of detail. The smaller the time unit, the larger the alphabet, and the more tracks coded, the more detailed the system is. This, in turn, affects coding time: detailed systems require significantly more time for data coding than less detailed ones (Birdwhistell, 1952; Bernardet et al., 2019; Dael et al., 2012; Ekman, Friesen, 1978; Farnell, 1996; Laban, Lawrence, 1974).

Reliability also varies across systems. Some, like FACS and BAP, have undergone empirical reliability evaluation, while others, like LMA, have been evaluated to a limited extent, and some systems have not been assessed for reliability at all (Bernardet et al., 2019; Dael et al., 2012; Ekman, Friesen, 1978; Laban, Lawrence, 1974; Shafir et al., 2016).

Thus, differences among movement classification, coding, and interpretation systems include their intended purpose, origin, degree of subjective inference, focus on movement quality or type, level of detail, coding time, and reliability. M. Karg et al. (2013) emphasize that movements are typically represented as joint angle trajectories or kinematic features, which, while detailed, can be computationally intensive and may overlook the expressive qualities of movements. Movement notation systems offer a more efficient and expressive representation.

Due to the conceptual proximity to our notation system, we pay particular attention to the Common Morphokinetic Alphabet (CMA) for transcribing and analyzing body movements, which seeks to provide a comprehensive, precise, and user-friendly method for recording physical movements, establishing grammatical rules based on Noam Chomsky’s phrase grammar (Izquierdo, Anguera, 2018). Like our notation, the CMA system incorporates linguistic principles, particularly the structure and syntax of movement phrases, to create a notation system capable of capturing the complexity of human movement in three-dimensional space over time (Izquierdo, Anguera, 2018). The CMA system builds on previous systems, such as Ray Birdwhistell’skinesic notation system (KNS) (Birdwhistell, 1952) and the Facial Action Coding System (FACS) (Ekman, Friesen, 1978), but positions itself as a more comprehensive and adaptable system capable of keeping pace with technological advancements (Izquierdo, Anguera, 2018).

It should be noted that the research conducted by Izquierdo, Anguera (2018) is closely related to our work in certain aspects, which will be discussed in the next section.

Methodology. Description of the Perm Gesture Notation (PGN)

The movement notation system, as we conceptualize it, must satisfy several key criteria.

First, the movement notation should be semantically oriented and based on natural language. This would allow subject matter experts, when writing or interpreting a movement formula, to visualize how the action will be performed. The language for recording movements should be represented as a formalized structure of concepts and rules for their implementation. This would facilitate the use of computational technologies, particularly allowing for encoded messages to be interpreted by an intelligent interpreter.

The language for recording movements must be flexible, extendable through the integration of new objects, concepts, and rules, and easily adaptable to changes in movement parameters. The notation should be comprehensive, covering all aspects of movement, and universal, capable of encoding all types of movements. Furthermore, the notation must exhibit anatomical and physiological accuracy, representing the mechanics of the body correctly. There should also be a possibility for quantitative evaluation of the generated movement models.

Additionally, the notation must be practical and easily integrated with modern technologies. It is crucial that the system of notation can document observed movements without relying on contextual assumptions or subjective interpretations, ensuring objectivity and minimizing coder bias. We have endeavored to account for these criteria as thoroughly as possible in the creation of our movement notation system.

Unlike other movement notation systems, particularly the Common Morphokinetic Alphabet (CMA) (Izquierdo, Anguera, 2018) , which is the closest to ours, where the movement notation includes not only position/state but also complex movement patterns (e.g., both hands together), with repetitions of entities (e.g., right and left sides for position and body parts), and where some indicators are described using numbers, our system models movement as a sequential transition from one stationary state of the body part performing the movement to another stationary state. The key distinction in our approach is that instead of describing the movement itself, which requires the inclusion of numerous variables, we define only the initial and final states of the body part performing the movement (intermediate states can be included, as discussed below) and the temporal characteristics of executing the movement as a transition from one state of the body part to another.

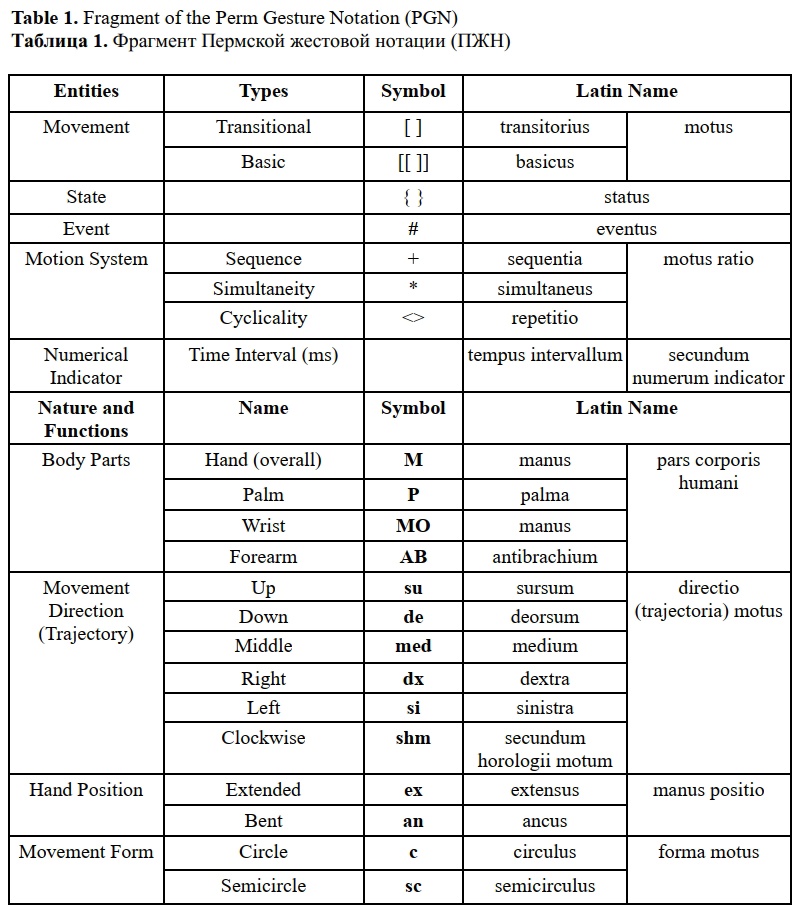
Each state has specific indicators associated with certain entities (movement system, numerical indicators, etc.), body parts, and their nature and functions. The entities, nature, and functions of body parts have different types, allowing them to be represented in a structured and symbolic form. Latin is chosen as the natural language for description. A fragment of the system is provided in Table 1.

The notation allows for the description of both complete movements and movement fragments. An example of a movement formula using our notation is:

:1000:{  } (1)

The description of movement using a specific notation system can be illustrated by the example of raising a hand, as shown in Figure 1. For the precise description of a body part’s state, the following model is used (demonstrated for the left hand):

● М (manus) – denotes the hand.

● Left lower index (si): Specifies the selected hand, where "si" means the left hand (similarly, "dx" refers to the right hand).

● Right upper index (ex): Indicates the hand’s position, where "ex" denotes an extended hand.

● Right lower index (de): Specifies the direction, where "de" means downward.

The use of curly braces {} around the notation indicates that this part of the movement represents a state, while :1000: specifies the duration of this state in milliseconds. Thus, formula (1) conveys the initial state of the movement.

This can be translated into a more machine-readable form as follows:

:1000:{_si_M^ex_de_} (2)

Some positions and states of the hand are assumed by default. For instance, the fully extended arm state is considered the default. Therefore, such states may not need to be explicitly marked in the notation. Consequently, formula (2) simplifies to:

:1000:{_si_M_de_} (3)

Using these notation rules, we can describe the movement shown in Figure 1 as follows:

 :1000:{_si_M_de_}:1000:[_si_M_su_]:1000:{RE} (4)

From this formula, it is clear that it does not describe intermediate states: the left hand moves directly from a downward extended position to an upward extended position. It may seem that the movement is described separately (e.g. 1000:[_si_M_su_]). However, this is not the case: this notation captures the final state as the result of the movement, and its placement within the movement code serves to: a) indicate the movement itself, b) specify its execution time, and c) allow for the possibility of simultaneous execution with another action (an example is provided below). At the same time, since the final state is already presented in the formula, there is no need to duplicate its notation, which is why the formula ends with the fragment 1000:{RE}, indicating that this state, lasting 1000 ms, is described in the movement block, i.e., as {_si_M_su_}.

Figure 1. Raising the Arm in Blender (three motion slices)

Рисунок 1. Поднятие руки в приложении Blender (три среза движения)

In this case, the movement is performed in the most efficient manner. However, if we want to execute the movement differently, we need to define intermediate states for the arm’s position. This will result in the arm moving along a different trajectory. For example, raising the arm through an intermediate position, where the arm is extended to the side, followed by a pause of 1 millisecond (1:{RE} denotes a resting state for 1 millisecond), can be described as follows:

:200:{_si_M_de_}:1000:[_si_M_si_]:1:{RE}:1000:[_si_M_su_]:200:{RE}

Figure 2. Raising an arm in Blender (four motion slices)

Рисунок 2. Поднятие руки в приложении Blender (четыре среза движения)

In Figure 2, it is evident that the final position of the arm coincides with the position shown in Figure 1: the arm is extended with the palm facing forward. To specify a different final position, we need to use additional notation to clarify the precise orientation, e.g.:

:200:{_si_M_de_}:1000:[_si_M_si_]:1:{RE}:1000:[_si_M_su*MO_dx_]:200:{RE}

Let’s examine the construction [_si_M_su*MO_dx_]:

● The final position of the left arm is indicated (upwards).

● The ‘*’ symbol denotes simultaneity, meaning another action occurs at the same time as the arm is in the upward position.

● “MO” represents the palm, and “dx” indicates that the palm is turned to the right. For the left arm, this means the palm is turned towards the body.

This example illustrates that the directions and positions of body parts, as described in Table 1, can be applied to various body parts depending on their anatomical capabilities. For instance, for the palm, “MO_at” (forward) indicates the arm is rotated so that the palm faces forward. Therefore, the position of the arm in its final state, as shown in Figures 1 and 2, can be precisely described using this notation system.

Since the notation is designed for modeling movements in computerized systems, there are preset configurations (settings) through which the movements of body parts in an anthropomorphic 3D model are executed. For example, raising the arm upward is performed through an intermediate state of elbow bending, thus such movement does not require special marking. At the same time, this approach raises the issue of determining the most human-like configurations, which can be achieved through statistical analysis of a wide range of human movements modeled with varying psychobiological characteristics (e.g., age, gender, temperament, etc.), a promising area for further research.

Up to this point, movement descriptions have been focused on a single body part. But how does the notation work with simultaneous movements of multiple body parts, such as both arms?

For modeling simultaneous-successional movements (simultaneous execution of actions by multiple body parts in their temporal dynamics), the following concepts are introduced:

1. Independence (autonomy) of the 3D model’s body parts, limited only by the anatomical and physiological capabilities of a human, as fixed in the 3D model settings.

2. “Recording tracks”, which are used for independent description of each body part’s movement (each body part is assigned its own “track”).

3. A movement event, understood as either: a) any change in state/movement of a body part caused by external factors (another body part or object, e.g., the hand striking another body part or object), or b) a complex movement of body parts, where mandatory states of these parts are defined relative to each other over time. It is worth noting that despite the autonomy of a body part’s movement, its motion can influence another body part due to connectivity and inertia (e.g., arm rotation affecting the torso). Such inertial changes are natural and are not considered events.

An event is tied to time but occurs within a certain interval Δt. The Δt parameters can be used to calculate and assess the precision of modeled movements. The event is denoted by the symbol "#" in the upper left index of the body part. For example, the description of the event (#1) where two hands make contact in front of the chest: for the left hand[_si_^#1^M_dx*at_]and for the right hand[_dx_^#1^M_si*at_]. Events have their indices, allowing distinction between different events and linking formula fragments describing various body parts.

It should be noted that complex movements (such as "hands together" in CMA) can be defined separately in our case and stored as formula variants. In other words, certain patterns of states or movements can be implemented as units in a dictionary, with their formal representations.

Implementation of Motion Control Systems

The development of a motion control system based on linguistic notation involves several stages: gesture notation, construction of an internal representation of motion, and its translation into executable movements, demonstrated using 3D modeling and animation software.

Stage One: Parsing Notation

The first stage is parsing the notation (formula parsing). Parsing involves analyzing the notation string, extracting terms, and creating an abstract syntax tree (AST). The parsing process is illustrated with the following formula example:

:400:{_dx_M_2la-de-2at_}:500:[_dx_M_la-su-2at_]:400:{RE}

1. Extraction of Individual Terms:

○ First Term: :400:{_dx_M_2la-de-2at_}

■ Time: 400 milliseconds.

■ Type: State ({})

■ Position Details:

■ dx_M: Right hand.

■ 2la: Movement left with coefficient 2.

■ de: Movement down.

■ 2at: Movement forward with coefficient 2.

■ Term Object: A State Term is created with attributes:

■ time = 400.

■ node = dx_M.

■ details = {‘2la’, ‘de’, ‘2at’}.

○ Second Term: :500:[_dx_M_la-su-2at_]

■ Time: 500 milliseconds.

■ Type: Movement ([])

■ Direction Details (Final State):

■ dx_M: Right hand.

■ la: Movement left.

■ su: Movement up.

■ 2at: Movement forward with coefficient 2.

■ Term Object: A Move Term is created with attributes:

■ time = 500.

■ node = dx_M.

■ details = {‘la’, ‘su’, ‘2at’}.

○ Third Term: :400:{RE}■ Time: 400 milliseconds.

■ Type: State ({})

■ Details: RE (State fixation).

■ Term Object: A State Term is created with attributes:

■ time = 400.

■ details = {‘RE’}.

Stage Two: Construction of Internal Motion Representation

In the second stage, an internal representation of motion is constructed based on the AST. This representation consists of a series of frames that include information about which body part of the performer is associated with each frame, how they affect its position, and the specific moment in time from the start of the motion when each frame is relevant. Only key frames are recorded in this series – extreme positions of primitive movements. E.g. if a performer needs to trace the letter “L” with their hand, the series will include key frames for the hand’s positions at the bottom, top, and top right. Motion interpolation is the responsibility of the performer.

Stage Three: Transformation of Internal Representation into Final Motion

The third stage involves transforming the internal representation into final motion. The internal motion representation is handed over to the performer, who converts it into the final result visible to the user. The performer can be a robot or any program working with skeletal animation, including game engines. In this study, Blender 3D, a 3D modeling and animation program, is used as the performer. Blender 3D allows for the creation of custom extensions using Python and provides a comprehensive set of graphical interfaces and software utilities for working with 3D graphics.

Results and discussions

In this paper, the results are presented as a demonstration of the notation’s ability to describe natural human movements extracted from video segments of a multimodal corpus depicting various emotional states described by individuals. The primary aim of the developed gesture notation is to facilitate seamless transitions from one form of human activity to another in different interface-mediated communications by providing a universal and precise system for encoding and describing human movements, including gestures, postures, and complex interactions of body parts.

At this stage, we do not aim for complete and precise tempo-rhythmic and spatial reproduction of human movements by machines due to existing technical limitations. Therefore, we will define the formal description boundaries: notation will be applied only to hand movements.

The complex of movements is described as a series of states for each hand, represented in two recordings (referred to as “tracks”). In formal notation, the transition from one track to another is separated by a comma (this symbol is used exclusively for this function).

The formal notation of the movement ultimately shapes our understanding of the gesture, which, from a semantic perspective, is communicatively directed and semantically coherent, and, from a formal perspective, represents a movement from one state to another (including intermediate states if present).

We examine fragments of movements from a specialized multimodal corpus of emotions and gestures. Emotions in this corpus can be broadly categorized as positive and negative. The quantitative and qualitative characteristics of the movements accompanying these emotions may vary. As an example, we consider two sets of movements: one associated with the positive emotion “Delight” (Figure 3) and another associated with the negative emotion “Anger” (Figure 4), as well as the corresponding linguistic contexts of their use (see Example 1 and Example 2). Illustrations will use screenshots of hand movement states from informants, which serve as model representations in the form of movement formulas.

Each of the movement complexes selected for illustration differs in several parameters. For the first complex, which occurs in the context of the emotion “Delight”, it is noted for its simplified structure. Additionally, this movement is an example of synchronous movement of both hands.

Figure 3. Illustration of the complex of movements within the framework of the emotion “Delight” and its components.

Рисунок 3. Иллюстрация комплекса движений в рамках эмоции «Восторг» и его составляющие.

This movement complex is observed in the following linguistic context:

Example 1. …И вот (Bent arms are folded with one palm placed on the back of the other hand palm) полет на параплане (Arms extended outward and downward), я была в восторге (Bent arms raised on either side)...

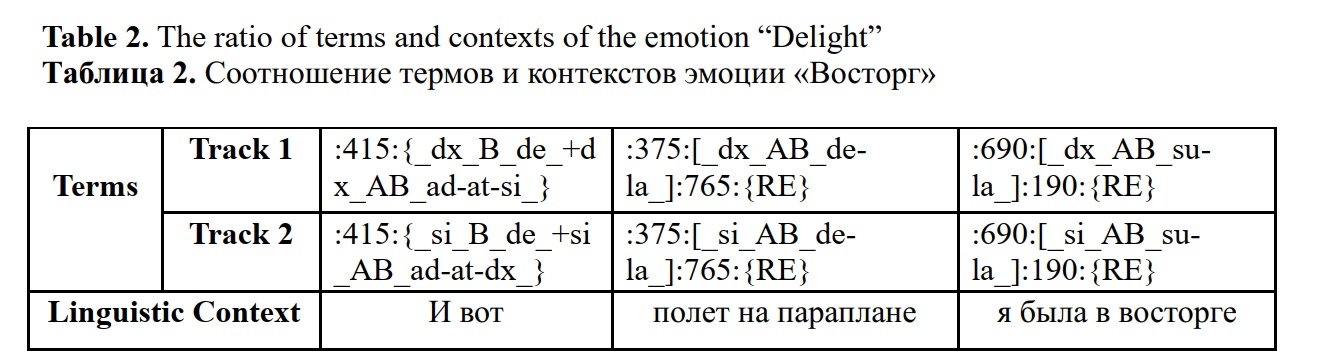
In describing the emotion “Delight”, the informant uses this movement complex (Figure 3), which can be divided into three main states: a) bent arms and one palm placed on the back of the other hand palm; b) arms extended outward and downward; c) bent arms raised on either side.

A detailed description of these states reveals the following characteristics: the initial state (a) represents the starting position where the arms are bent at the elbows at a 90-degree angle, with the left forearm directed forward and to the right, the right forearm forward and to the left, and the palms pressed together at the level of the abdomen (palms up). This component can be represented by the terms ({_dx_B_de_+dx_AB_ad-at-si_} and {_si_B_de_+si_AB_ad-at-dx_}). In state (b), the right arm is extended downward and to the right, and the left arm is extended downward and to the left ([_dx_AB_de-la_] and [_si_AB_de-la_]). Finally, the last state (c), which is the concluding stage of the complex, is characterized by the right arm being bent with the forearm directed upward and to the right, and the left arm also bent with the forearm directed upward and to the left ([_dx_AB_su-la_] and [_si_AB_su-la_]). Each part of the movement component is followed by a fixation with a specific time measurement, e.g. (:190:{RE}).

This movement complex can be clearly encoded as the following formula:

:415:{_dx_B_de_+dx_AB_ad-at-si_}:375:[_dx_AB_de-la_]:765:{RE}:690:[_dx_AB_su-la_]:190{RE},:415:{_si_B_de_+si_AB_ad-at-dx_}:375:[_si_AB_de-la_]:765:{RE}:690:[_si_AB_su-la_]:190:{RE}

The structure of this formula consists of six terms, three for each hand. These terms are distributed across two tracks, one for the right hand and one for the left hand, respectively. Comparing the terms and their sequences across both tracks reveals their complete identity, indicating the synchronicity of the movements of both hands. Furthermore, each term can be associated with a specific linguistic context, as illustrated in Table 2.

The following section presents an illustration of the movement complex accompanying the negative emotion “Anger”.

Figure 4. Illustration of the complex of movements within the framework of the emotion “Anger” and its components.

Рисунок 4. Иллюстрация комплекса движений в рамках эмоции «Злость» и его составляющие.

The complex movement patterns associated with the emotion of “Anger” are accompanied by the following linguistic context:

Example 2. (Both hands are lowered) Злость – это когда постоянно хочется прямо подраться (Hands bent, the forearms of the right and left arms are lifted upwards and come together – right to the left, left to the right) или ты хочешь (Right hand bent, forearm upward, left hand extended downward and slightly to the side) стукнуть по столу (Bent hands are stacked, one palm in a fist on top of the other), сказать (Right hand bent, right forearm to the left and slightly up, left hand extends forward, to the right, and then drops down with a five-fold amplitude), что нет (Hands extended downward and diverge – right to the left, left to the right, and cross), ты не прав…

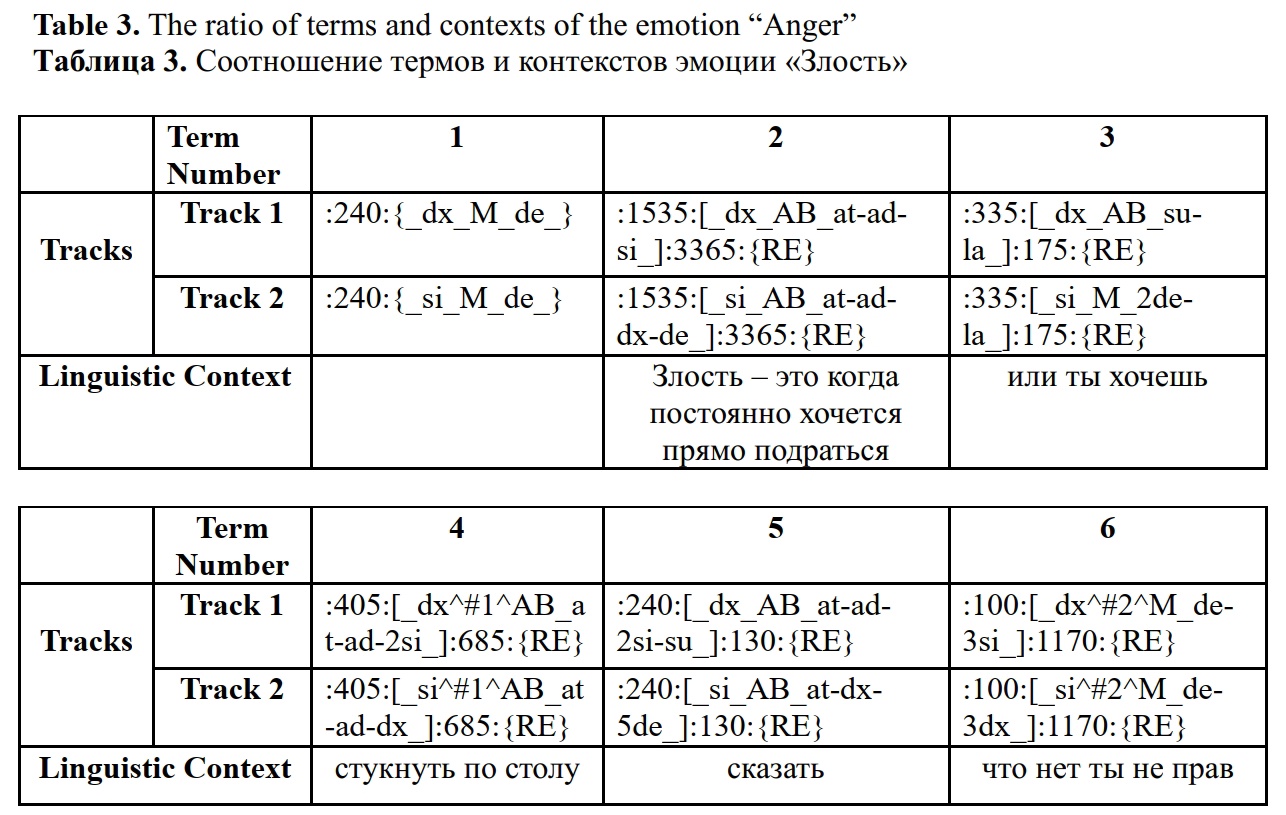
The interpretation of movements in this sequence, as opposed to the previous one, is more complex, involving unsynchronized and additional actions for the right (dx) and left (si) hands, structured by terms in two main tracks.

For the right hand, movement begins from the initial position with the hand lowered down ({_dx_M_de_}). This is followed by several components. The second component (b) ([_dx_AB_at-ad-si_]) is observed when the right forearm extends forward, bends towards the shoulder, and moves left, after which the final position is fixed ({RE}). Next is the third component (c) – the forearm raises up and moves left ([_dx_AB_su-la_]), also followed by fixation ({RE}).

The first event (d) ([_dx^#1^AB_at-ad-2si_]) involves the forearm extending forward, bending towards the shoulder, and moving left with double amplitude. After fixing the position (:200:{RE}), we encounter the next component (e) ([_dx_AB_at-ad-2si-su_]), where the forearm again extends forward, bends towards the shoulder, moves left with double amplitude, and then rises. The stage ends with fixation ({RE}). The final event (f) includes lowering the hand down and moving left with triple amplitude ([_dx^#2^M_de-3si_]), followed by fixation ({RE}).

The left hand repeats a similar sequence of movements. In the initial position (a) it is also lowered down ({_si_M_de_}). The next component (b) includes extending the forearm forward, bending towards the shoulder, moving right, and lowering down ([_si_AB_at-ad-dx-de_]), after which the position is fixed ({RE}). Next (c), the forearm lowers down with double amplitude and moves left ([_si_M_2de-la_]), with fixation ({RE}).

The first event (d), where the forearm extends forward, bends towards the shoulder, and moves right, can be noted as ([_si^#1^AB_at-ad-dx_]), with subsequent fixation ({RE}). Then follows the movement component (e), where the forearm extends forward, moves right, and lowers down with five-fold amplitude ([_si_AB_at-dx-5de_]), after which the position is fixed ({RE}). The final event (f) includes lowering the hand down and moving right with triple amplitude ([_si^#2^M_de-3dx_]), ending with fixation ({RE}).

The overall description of this movement complex, considering its temporal range, can be encoded as follows:

:240:{_dx_M_de_}:1535:[_dx_AB_at-ad-si_]:3365:{RE}:335:[_dx_AB_su-la_]:175:{RE}:405:[_dx^#1^AB_at-ad-2si_]:685:{RE}:240:[_dx_AB_at-ad-2si-su_]:130:{RE}:100:[_dx^#2^M_de-3si_]:1170:{RE},:240:{_si_M_de_}:1535:[_si_AB_at-ad-dx-de_]:3365:{RE}:335:[_si_M_2de-la_]:175:{RE}:405:[_si^#1^AB_at-ad-dx_]:685:{RE}:240:[_si_AB_at-dx-5de_]:130:{RE}:100:[_si^#2^M_de-3dx_]:1170:{RE}

Based on the presented formula, it is noted that the examined sequence represents a complex hand movement pattern, which includes not only elementary manipulations but also more complex forms of interaction between the hands, indicating a high level of coordination and synchronization of movements within this sequence. Thus, it can be emphasized that the proposed gesture notation is an effective tool for systematizing and displaying not only primitive but also complex movements. This notation allows for accurate and detailed recording of any gesture interactions, ensuring a precise representation of their structure and sequence.

The notations presented in Tables 2 and 3 can be enriched with additional parameters. The first set consists of dynamically variable behavioral parameters, based on the already identified parameters (sequence of terms in the formula, speech material, duration of gestures), and includes metrics derived from these parameters, as well as optional physiological characteristics that can be measured in experimental situations (pulse, tidal volume, saturation, etc.). The second set consists of optional constants (for ongoing communication) describing socio-demographic, psychological, and physiological parameters of the individual (gender, age, education, height, arm span, etc.).

The construction of a hierarchy of metrics for gesture analysis and their constraints relies on extensive research materials. Recent studies (Liu et al., 2022; Qi et al., 2024; Tonoli et al., 2024; Yang et al., 2023; Yoon et al., 2020; Zhi et al., 2023) discuss metrics such as Mean Squared Error (MSE), Mean Average Error (MAE), Fréchet Gesture Distance (FGD), Gesture Area Coverage (GAC), among others, which compare movements to a reference, assess naturalness and similarity, analyze dynamic characteristics (speed, acceleration, etc.), and consider spatial coverage of gestures.

It is proposed that some metrics might also be used for evaluating speech-gesture behavior. Assuming that the integral behavioral unit is the term (as a final state of movement, represented in notation by a transition from the previous state to the next via movement, i.e., as {termK} → [termK+1]), all measurements should be tied to terms. This approach leads to the following metrics:

1. L – Length of the hand movement trajectory. Calculations can be performed for a segment (termK → termK+1) as well as for the entire chain of movement for one or both hands: term1 → term2 →… → termN.
2. S – Area under the curve of the hand movement trajectory within a single gesture, i.e., the designated behavioral unit termK → termK+1, and for the entire movement.
3. V – Volume of space captured by the gesture (termK → termK+1). Measurement methods may vary from the space of a single hand or both hands to the space considered between two hands in the gesture.

Parameters L, S, and V require normalization in the description of real communication (without using 3D models); we propose introducing a normalizing parameter , where (l1 – height, l2 – arm span) for L, N² for S, and N³ for V.

4. speech – Volume of speech material associated with the duration of the gesture, i.e., termK → termK+1.

5. temp – Metric characterizing the dynamics of the space captured by gestures: . The temp metric can also be computed differently, such as the ratio of the number of terms or volume of speech material to the unit of time.

Overall, the recording of the function arguments for Behavior can be represented as follows:

Behavior = {(term₁, speech₁, t₁, L₁, S₁, V₁, …),..., (term_N, speech_N, t_N, L_N, S_N, V_N, …); (pulse₁, tidal volume₁, ...)*, ..., (pulse_N, tidal volume_N, ...)*; (gender, age, N, temp...)*}, where the asterisk (*) denotes groups of optional parameters.

Conclusions and Future Work

The creation of a formalized system for encoding human movements for interface-mediated communication in various machine-generated environments, as we have attempted to demonstrate, is a complex yet solvable scientific problem. In the course of the study, the Perm Gesture Notation system was introduced, and the unit for describing human behavior – the term – was identified. A term represents the record of a transition from a preceding fixed state of a body part within its movement to a subsequent fixed state. As a unit of movement discretization, a term aligns with other forms of activity (i.e., it functions as a cognitive-behavioral unit), such as speech (we discussed the volume of speech material, though other measurable parameters, such as acoustic measures, may also be relevant), as well as facial expressions or data from wearable devices that convey information about pulse, breathing volume, and other factors.

Given that each human movement likely has semantic meaning, i.e., is not random and/or chaotic in the sequence of human behavior acts, we should ultimately require machines to achieve similar semantic understanding of motor activity and synchronize it with the speech semantics of the message. Complete and accurate tempo-rhythmic and spatial reproduction of human movements by a machine (i.e., essentially replicating the human chronotope by its virtual avatar) can be achieved by combining computer vision methods with modern neural network transformer models. The ultimate goal of this approach is to generate a movement formula in the developed formal language notation based on the analysis of video sequences of human movements input into the model. The generated formula can then be transmitted to an executor (either a virtual 3D model or a physical robotic device). Reproducing the encoded movements by the executor is necessary for analyzing the accuracy and realism of the generated animations through comparison with actual movements, followed by formula adjustments and model retraining.

It is evident that the quality of the model’s reproduction of human speech-gesture behavior by the machine should ultimately be assessed by humans themselves. It is important that machines not only replicate physical movements but also appropriately convey the semantic and emotional values of these movements, in accordance with human expectations and cultural norms. In this context, there is a need to develop a separate branch of general semantics – technosemantics, as semantics generated by anthropomorphic machines in human-machine interaction and directed towards the communicating human (for issues related to technosemantics, see (Belousov et al., 2024)).

The synthesis of movements, which is oriented not only towards mechanical reproduction but also towards meaningful content, is a crucial component in creating more effective and human-centered communication systems in various machine-generated environments. It is important to consider not only visual and kinematic parameters but also the hidden meanings carried by gestures and movements in the context of communication. This task becomes increasingly relevant in the context of the development of anthropomorphic machines and large language models, which strive not only to imitate humans but also to communicate with them at a level close to human interaction.

In conclusion, further development of movement encoding systems, including those presented in this work, and their application in various fields such as the film industry, computer games, education, medicine, sports, and robotics, could lay the foundation for new forms of communication where machines not only execute commands but also actively engage in semantically meaningful interactions, maintaining a comprehensive and intuitive dialogue with humans.